Awasome Acceleration Vector Ideas

Awasome Acceleration Vector Ideas. (4.3.4) a → = a 0 x i ^ + a 0 y j ^. The acceleration vector is the rate at which the velocity vector is changing (with respect to time):

Why Is Acceleration A Vector at Collection of Why Is from vectorified.com

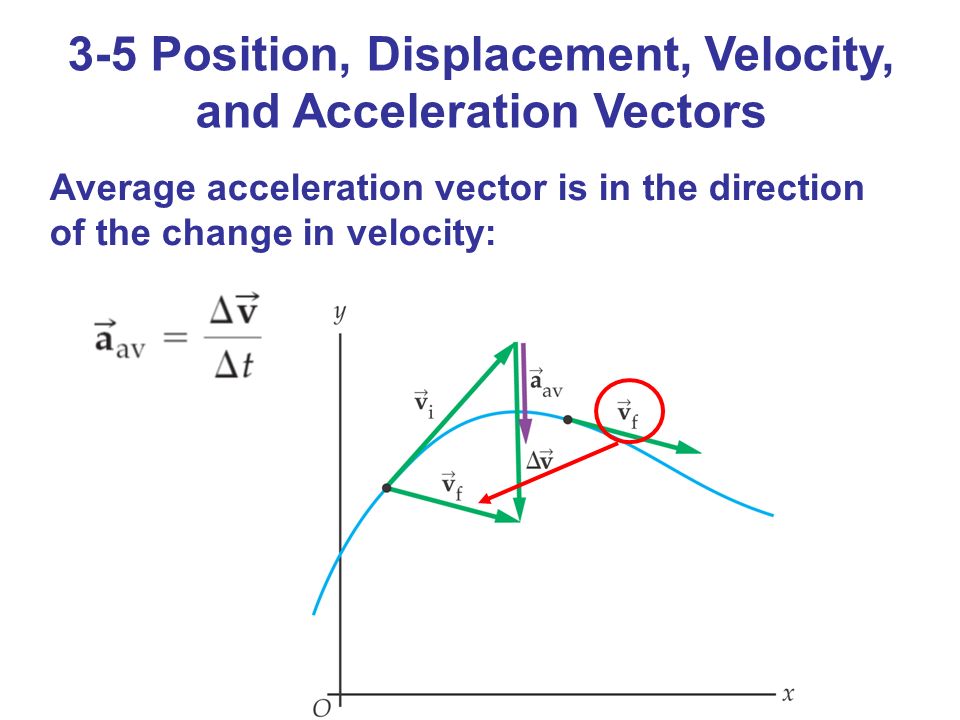
Describe the motion of a particle with a constant acceleration in three dimensions. The relationship between displacement, r r, velocity, v v and acceleration, a a is the same when the quantities are represented as vectors or as scalars. The motion of a particle is described by three vectors:

Source: www.researchgate.net

Suppose that we know the cartesian coordinates, , , and , of this body as time, , progresses. R ( t) = 2 t 2 i + 4 t j + 3 t 3 k r (t)=2t^2\bold i+4t\bold j+3t^3\bold k r ( t) = 2 t 2 i + 4 t j + 3 t 3 k.

Source: www.airports-worldwide.com

The components of the position vector are time dependent since. We’ll start by finding r ′ ( t) r' (t) r ′ ( t), the derivative of the position function.

Source: vectorified.com

Therefore we can write velocity and acceleration as v. The centripetal and the tangential.centripetal acceleration changes the direction of the velocity, and therefore the shape of the track, but doesn't affect the value of.

Source: www.researchgate.net

Acceleration is a vector as it is always associated with force. The relationship between displacement, r r, velocity, v v and acceleration, a a is the same when the quantities are represented as vectors or as scalars.

Source: vectorified.com

Summary in two and three dimensions, the acceleration vector can have an arbitrary direction and does not necessarily point. (4.3.4) a → = a 0 x i ^ + a 0 y j ^.

Source: www.createmepink.com

The only difference in two or three dimensions is that these are now vector quantities. Calculate the acceleration vector given the velocity function in unit vector notation.

Source: vectorified.com

Vector velocity and vector acceleration. The definition of acceleration can be stated as:

Source: physics.stackexchange.com

Sports announcers will occasionally say that a person is accelerating if he/she is moving. The motion of a particle is described by three vectors:

Source: stackoverflow.com

The acceleration vector is the rate at which the velocity vector is changing (with respect to time): * * demonstration of the basics of motion with vector.

Usually, We Have Two Parts That Are Perpendicular To Each Other:

Occasionally sports announcers say that a person is accelerating if they are moving fast. Learning objectives calculate the acceleration vector given the velocity function in unit vector notation. The magnitude of an object's acceleration, as described by newton's second law, is the combined.

Therefore We Can Write Velocity And Acceleration As V.

An object is still accelerating if it is changing its velocity time and again. Centripetal acceleration and tangential acceleration. Sports announcers will occasionally say that a person is accelerating if he/she is moving.

Calculate The Acceleration Vector Given The Velocity Function In Unit Vector Notation.

Mathematically, v → = r → d t. A → = v → d t. The relationship between displacement, r r, velocity, v v and acceleration, a a is the same when the quantities are represented as vectors or as scalars.

The Definition Of Acceleration Can Be Stated As:

The cartesian components of this vector are given by: Understand how velocity and acceleration can be represented using vectors. Accelerations are vector quantities (in that they have magnitude and direction).

An Object Is Accelerating If It Is Changing Its Velocity.

The instantaneous acceleration is produced by a change in velocity taken over a very short (infinitesimal) time period. Summary in two and three dimensions, the acceleration vector can have an arbitrary direction and does not necessarily point. The centripetal and the tangential.centripetal acceleration changes the direction of the velocity, and therefore the shape of the track, but doesn't affect the value of.