Incredible Matrix Multiplication Vs Cross Product References

Incredible Matrix Multiplication Vs Cross Product References. The main attribute that separates both operations by definition is that a dot product is the product of the magnitude of vectors and the cosine of the angles between them whereas a cross product is the product of magnitude of vectors and the sine of the angles between them. Two vectors have the same sense of direction.

NumPy Vector Multiplication from www.geeksforgeeks.org

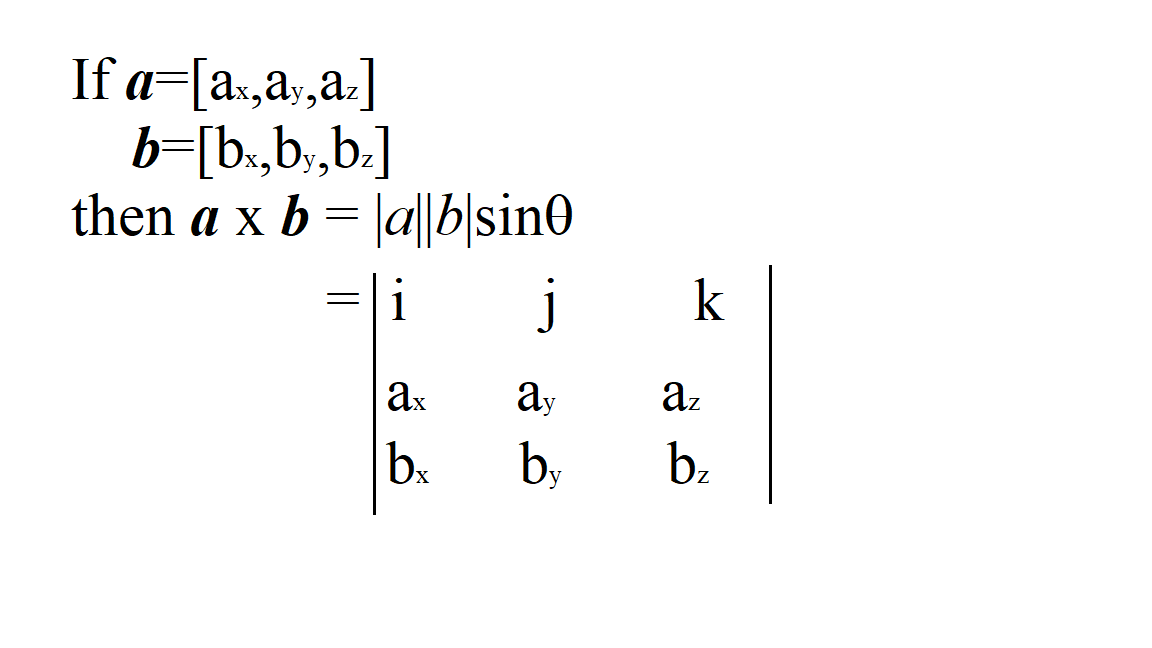
This is the required matrix after multiplying the given matrix by the constant or scalar value, i.e. The way i understand it, a formal dot product of matrices a and b that have the same number of columns is a.b=a t b, where t is the transpose operation; #it_officialsin this video i will show you what is the difference between matrices multiplication, cross product and dot product in matlab | matrix division.

Source: betterexplained.com

Try and make this a tab bit more clear. \{a_1, \dots, a_m\} and \{b_1, \dots, b_l\}.

Source: culcal.blogspot.com

Conversely, if two vectors are parallel or opposite to each other, then their product is a zero vector. A vector has magnitude (how long it is) and direction:.

Source: math.stackexchange.com

If we take two matrices and such that = , and , then. 3 × 5 = 5 × 3 (the commutative law of multiplication) but this is not generally true for matrices (matrix multiplication is not commutative):

Source: culcal.blogspot.com

Suppose you have two groups of vectors: W × v = [ w] × v = [ 0 − w 3 w 2 w 3 0 − w 1 − w 2 w 1 0] v.

Source: medium.com

The result of this dot product is the element of resulting matrix at position [0,0] (i.e. Now depending on whether you assume w 2 ≠.

Source: www.geeksforgeeks.org

Multiplication of two matrices involves dot products between rows of first matrix and columns of the second matrix. 18) if a =[aij]is an m ×n matrix and b =[bij]is an n ×p matrix then the product of a and b is the m ×p matrix c =[cij.

Source: culcal.blogspot.com

W × v = [ w] × v = [ 0 − w 3 w 2 w 3 0 − w 1 − w 2 w 1 0] v. Matrix product (in terms of inner product) suppose that the first n × m matrix a is decomposed into its row vectors ai, and the second m × p matrix b into its column vectors bi:

Source: www.slideserve.com

Try and make this a tab bit more clear. D=ax (b*c) how would i solve for c?

Source: thaipoliceplus.com

W × v = [ w] × v = [ 0 − w 3 w 2 w 3 0 − w 1 − w 2 w 1 0] v. Now depending on whether you assume w 2 ≠.

When Taking The Dot Product Of Two Matrices, We Multiply Each Element From The First Matrix By Its Corresponding Element In The Second Matrix And Add Up The Results.

In arithmetic we are used to: Two vectors have the same sense of direction. To perform multiplication of two matrices, we should make sure that the number of columns in the 1st matrix is equal to the rows in the 2nd matrix.therefore, the resulting matrix product will have a number of rows of the 1st matrix and a number of columns.

The Cross Product A × B Of Two Vectors Is Another Vector That Is At Right Angles To Both:.

Matrix multiplication represents the composition of 2 (or more) transformations, so is not the same thing!.show more. On the other hand, the cross product can be represented as a × b = ab sinθ n. A × i = a.

If A And B Are Vectors, Then They Must Have A Length Of 3.

A b a b proj b a it turns out that this is a very useful construction. B = ab cos θ. Thankyou, this makes sense i think i was just being a little thick.

Matrix [ W] × Has Rank 2 And Its Nullspace Is Spanned By [ W 1, W 2, W 3] ⊤.

The result of this dot product is the element of resulting matrix at position [0,0] (i.e. The vector cross product takes 2 vectors as input and produces a third vector orthogonal to the other two. If i have the following 4 vectors:

More Explicitly, The Outer Product.

In mathematics, particularly in linear algebra, matrix multiplication is a binary operation that produces a matrix from two matrices. As we know, sin 0° =. A b a b proj a b alternatively, the vector proj b a smashes a directly onto b and gives us the component of a in the b direction: